Lau Pak To (Ryan)

Topological Edge Modes in Non-Hermitian 1D Fermionic Spin Chains

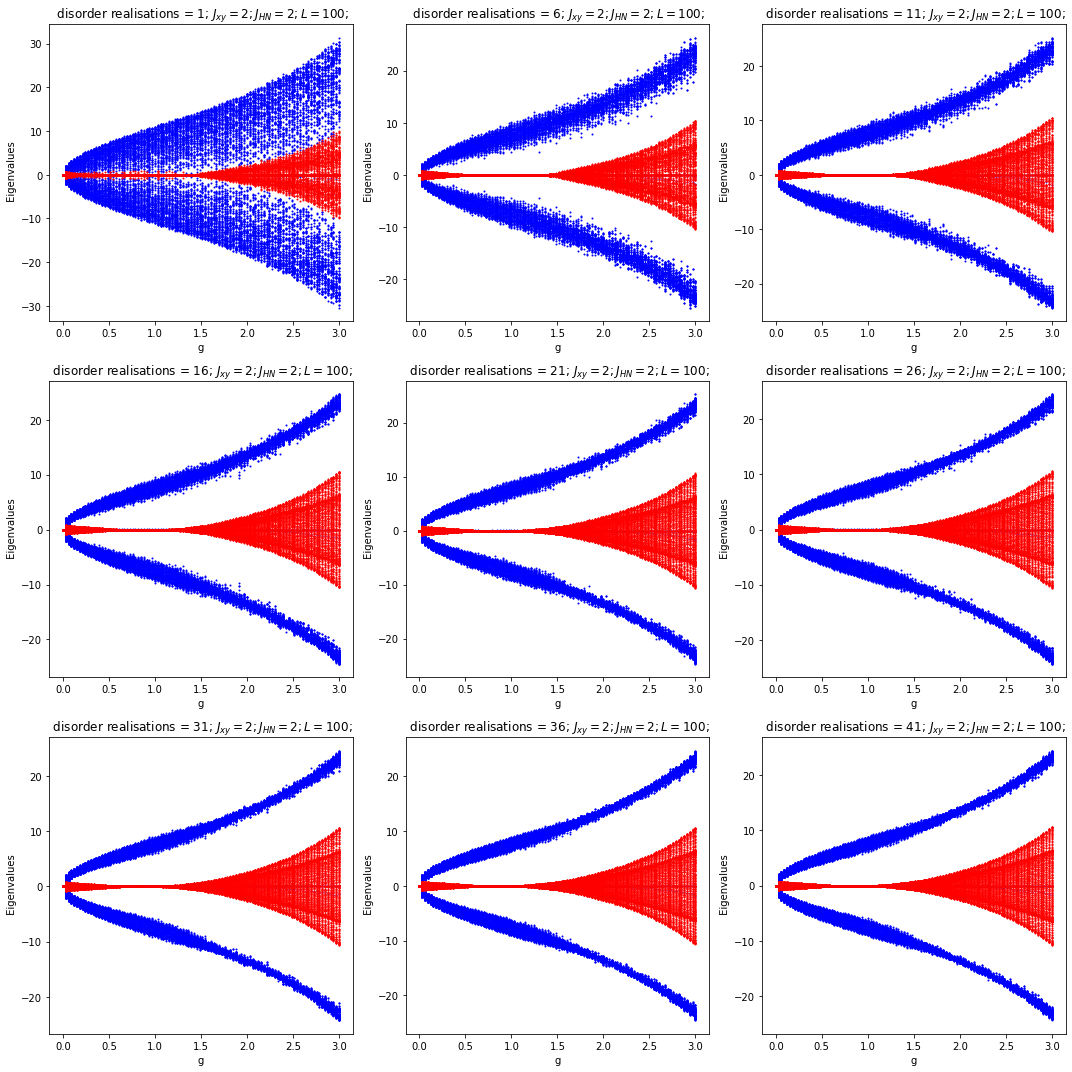
The energy dispersion against asymmetric hopping strength of the suggested disordered XY-Hatano-Nelson model with open boundary conditions. Blue dots are real part of eigenenergies and red dots are imaginary parts of the eigenenergies.

Supervisor: Dr. Arijeet Pal

Dissertation title : Topological Edge Modes in Non-Hermitian 1D Fermionic Spin Chains
Abstract:
Quantum computers have huge potential to help humanity solve real world problems as they have great promises to be much more efficient than classical computers. Therefore, quantum computation has been an active area of research worldwide, striving to build the perfect fault-tolerant quantum computer. The major setback to this is that qubits as quantum systems are vulnerable to thermalisation and decoherence. There has been great success in using quantum error correction to account for such errors. In this work, we aim to improve qubits by focusing on the problem with decoherence, which can be realistically modelled by non-Hermitian, open system dynamics. More specifically, qubits can exist in edge modes in quantum spin systems. In 1D Hermitian systems, edge states are protected by the systems' intrinsic symmetries and such states are deemed to be Symmetrically Protected Topological (SPT) phases. In non-Hermitian cases in 1D, richer topological phases can be recognized and explored. Two 1D fermionic non-Hermitian models have been investigated in this thesis: the 1D Floquet transverse field Ising (F-TFI) model and the Hatano-Nelson model with XY interactions (XYHN) with on-site disorder. In these non-Hermitian models, edge states with purely real energies are present with certain protections. More interestingly, the edge modes in the XYHN model persist and are more localized in the presence of disorder, showing the non-Hermitian skin effect. This work has great implications as it grants more knowledge on non-Hermitian dynamics in spin systems, which can be adapted and applied to real-world quantum technology purposes. For example, the protected edge states can not only be a perfect candidate for qubits in quantum computers, but also a good resource for more efficient storage of information. At the end of the report, potential future work will be suggested for further improvements and extensions, ending with a conclusion.

Literature Review: On the potential of Topological Time Crystals for Quantum Error Correction
Review Brief:
Since the 1980s, it has been speculated that quantum computers can be used to simulate systems, solving physics and chemistry problems. With the impressive works in recent years, theoretical, computational and experimental techniques have been developed, all in the hopes of reaching quantum “supremacy”. Still, there are engineering and theoretical challenges in building a scalable fault tolerant quantum computer, as quantum states in its processors are vulnerable to noises and decoherence. Error correction codes can help protecting information loss and performing error-free computation, with the toric code as the most well-known examples. Being robust to perturbations, the toric code is a 2D topologically ordered quantum matter. We extend this idea to another type of exotic phases of matter, known as time crystals. First proposed by Frank Wilczek, time crystals are periodically driven systems which break continuous time symmetry rather than translational symmetry in classical cases. Forming a dynamical phase of matter, time crystals are protected via many-body localisation. Recent works have shown that there exist topological time crystals. We look into the possibility that error correcting codes can be realised in such exotic systems which could be used for error correction. Moreover, quantum memory encoded in the system may be preserved via topological protection and many-body localisation. This literature review introduces a novel solution to fault-tolerant quantum computation and information processing. This has huge implications in the quantum technology industry, as these fault tolerant quantum computers will help solve many problems much more efficiently than classical ones, such as optimisation problems, quantum machine learning, quantum chemistry, drug discovery many-body physics problems.

Quantum Simulations of Antigen-Antibody reactions

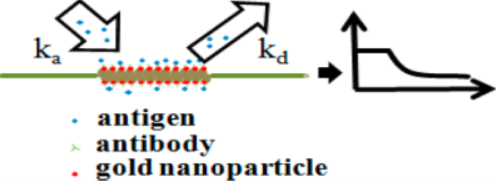
Image from: Chang, T.-C., Wu, C.-C., Wang, S.-C., Chau, L.-K. & Hsieh, W.-H. Using a fiber optic particle plasmon resonance biosensor to determine kinetic constants of antigen–antibody binding reaction. Analytical Chemistry 85, 245–250 (2012).

Supervisor: Dr Po-Heng (Henry) Lee

Project Brief:
An exploratory and consulting project, assisting a company to understand the interactions between antigen-antibody reactions on a gold nanoparticle surface using density matrix methods.

Q-Wave: Simulating sound waves using Quantum Algorithms

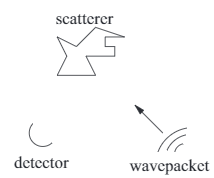
Image from: P.C.S. Costa, S. Jordan, and A. Ostrander, Quantum algorithm for simulating the wave equation, Phys Rev. A 99, 012323 (2019).

Supervisor: Dr. Reza Haqshenas

Project Brief:
Wave equations are well-known to describe physical waves. In this research, we hope to solve a particular form of the wave equation, known as the Helmholtz equation, in 2 dimensions. We will be using the HHL algorithm to solve the equation in the frequency domain.
A report is written as a summary. A software package written in Python, named "QWave", is in its initial developmental stage and is yet to be published for public use.

Classifying Topological Phases of Quantum Matter using Tensor Networks

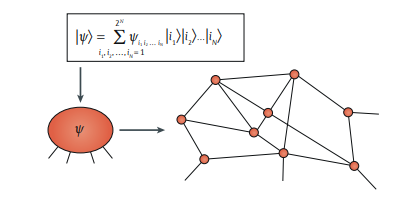
Image from: Orús, R. Tensor networks for complex quantum systems. Nat Rev Phys 1, 538–550 (2019).

Supervisor: Professor Andrew Green

Abstract:
It is long thought that Landau’s symmetry-breaking theory can help classify all phases of matter. However, this theory is incomplete. Quantum topological phases of matter are phases of matter which cannot be classified using this spontaneous symmetry-breaking theory, and are robust against perturbations. They have great significance in quantum technologies. Mathematical objects known as tensor networks can help us classify these phases of quantum matter. In this review, we discuss the ideas surrounding topological matter and tensor networks by providing analogies and examples. We focus on how tensor network methods can be used to classify topological phases of matter. Its significance in quantum technologies and the uses of tensor network beyond classification are discussed. The potential future works are identified and outlooks of the subject are given. The reference section at the end gives a list of literature for further reading.

Please feel free to contact me if you would like to see my literature review

Topological Phase Transition in S=1/2 spin chains with alternating ferromagnetic (FM) and antiferromagnetic (AFM) couplings and exchange anisotropy

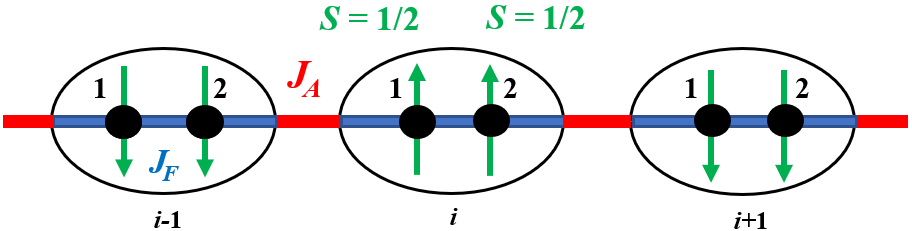
Supervisor: Dr. Frank Kruger

Abstract:
A 1D S=1/2 spin chain with alternating FM and AFM couplings is investigated in the limit of small magnetic anisotropy. The model is treated in terms of a simple nearest-neighbour hamiltonian, then performing a Jordan-Wigner transformation to map the spin 1/2 operators to spinless fermions. In the regime of strong anisotropy (XY case), fermions will be non-interacting and is exactly solvable. The model will be equivalent to a Haldane spin chain, exhibiting topological order, hence will be stable against small perturbations. Interactions of the studied regime is treated in a mean-field approximation, requiring to solve coupled self-consistency equations numerically using Python and Mathematica. The topological phase boundary is determined numerically using a bisection method as a function of the relative strength of the exchange coupling and the magnetic exchange anisotropy.

A one page report is written as a summary, with a more detailed appendix explaining the steps I took.

The 3-Coloured Distributive Consensus Problem

Supervisor: Hatem Elshatlawy & Stephen Wolfram

Brief Introduction to the Wolfram Physics Project (WPP):
Since Sir Issac Newton developed the foundations of mathematical physics, mathematics has been used extensively to model natural phenomenon. To investigate what nature does, equations have to be derived and solved, and so the fundamentals of physics are described using mathematics. The WPP implements a unique approach to discover and explain the fundamental theory of physics in terms of graphs, hypergraphs, rules and computations, while conforming with modern mathematics. A very important principle to bear in mind is that simple rules produce complex behaviours. For example, cellular automaton has shown to demonstrate phase transition behaviours in the 2D Ising Model (see link), which closely relates to my project. My aim was to find a rule that generates similar phase transistion behaviours, but in a 3-colored case.

For more information about WPP, this piece of writing from the CEO of Wolfram Research, Dr. Stephen Wolfram, which I think summaries the WPP very well: Even beyond Physics: Introducing Multicomputation as a Fourth General Paradigm for Theoretical Science

Abstract:
Consider a collection of cells with a certain fraction of 3 distinct colours. It is hypothesised that some rule, of which when applied to the system, will turn all the cells to the majority colour when that fraction of the colours exceeds a certain threshold, reaching global consensus. The system will also exhibit indeterminate states when there are equal weights of colors, or ”phase transitions”. A general majority rule has been hypothesised and studied using grid cellular automata and Mathematica, in cases of 2 and 3 colors.

Link for the report, featured in the Wolfram Community, with a staff picked Featured Contributor Badge: https://community.wolfram.com/groups/-/m/t/2312007